Els gràfics nostres de cada dia

Pintar un quadre és fàcil, el més bàsic consisteix en llençar un pinzell contra el llenç, una altra cosa és pintar un bon quadre. Amb els gràfics dels fulls de càlcul igual, amb tres clics ja se’n pot fer un. Una altra cosa és adaptar-lo perquè l’usuari capti l’essència del que volem transmetre i ho faci gairebé d’un cop d’ull.

Mostrar informació numèrica en un gràfic és la manera visual de sintetitzar informació, que ens ha de permetre transmetre una o més idees fàcilment en front de forçar al destinatari a memoritzar una relació de dades i/o text. Si ha de suposar un esforç d’interpretació pel destinatari no és un bon gràfic, o bé no s’ha utilitzat l’idoni.

En aquest post detallem tres exemples de graficació d’informació numèrica amb el full de càlcul més estès, que és prou versàtil per a fer bona part dels gràfics dels informes socioeconòmics, estudis d’investigació social, etc.

Les icones

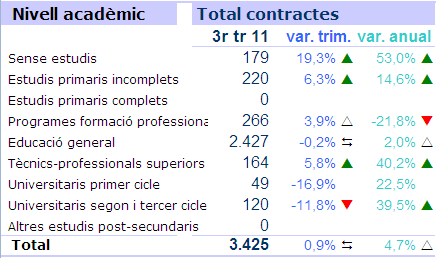
El “format condicional” és una eina molt útil per visualitzar informació numèrica sense haver de fer un gràfic, amb força combinacions d’icones i formats. Sovint ens podem trobar, però, que la combinació que volem no es troba entre les predeterminades o que simplement volem un disseny diferenciat. És possible a partir d’una fórmula i un format determinat mostrar amb icones un interval de valors. Un exemple és la taula de sota “Nivell acadèmic”, on les icones (triangles) es modifiquen en funció de la xifra absoluta i de la variació percentual, amb la fórmula condicional:

=SI(E9<51;" ";SI(F9>0,05;"p";SI(F9>0,01;"r";SI(F9>-0,01;"D";SI(F9>-0,05;"s";"q")))))

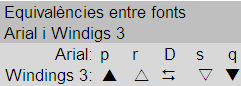
El primer condicionant de la fórmula determina si ha d’aparèixer o no una icona (entre les cometes hi ha un espai), en l’exemple d’aquesta taula, per sota del valor 51 es considera que millor no aparegui. Els següents condicionants determinen quina lletra/icona apareixerà. La fórmula no accepta directament icones però s’hi poden posar lletres a les que, aplicant una altra font de lletra, es converteixen en les icones que volem (vegeu “Equivalències entre fonts Arial i Windings 3”). Un cop donem el format de color al triangle el programa els atribueix directament en les cel·les contigües.

      

Variables de diferent nivell

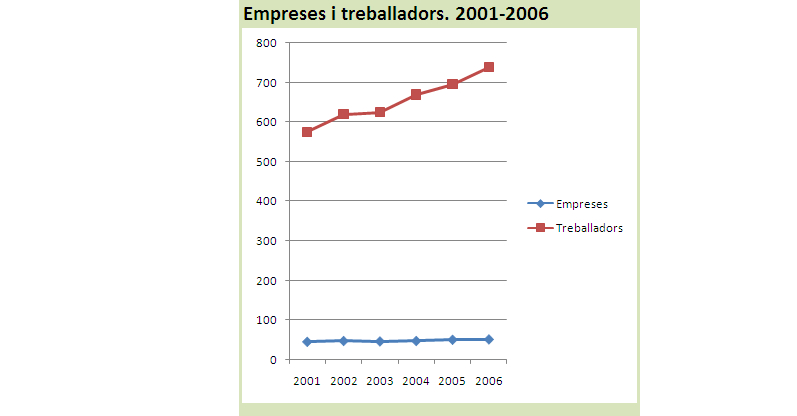
Sovint volem comparar l’evolució de dues variables que estan relacionades, com empreses i assalariats o renda i consum. Si tenen nivells força diferents al fer-ne un gràfic pot ser que l’ull humà no distingeixi si una variable ha augmentat o s’ha mantingut estable (vegeu variable “Empreses” al gràfic de sota, dades inventades per l’exemple). Si com a destinataris del gràfic no tenim més dades interpretarem que mentre les empreses s’han mantingut estables, el nombre de treballadors ha augmentat aproximadament un terç. L’habitual és que el gràfic vagi acompanyat d’un text explicatiu on apareguin les taxes de variació, però si el gràfic no sintetitza i millora el text o la relació de dades en una taula, no paga la pena fer-lo.

Una bona opció per visualitzar conjuntament l’evolució de dues variables de diferent nivell és l’ús d’un segon eix, “eix secundari”. Pot ser una bona opció si es té en compte un aspecte important: el quocient entre el nivell màxim i mínim dels dos eixos d’ordenades ha de ser el mateix. Dels dos gràfics de sota, el de l’esquerra no ho compleix atès que 780/540 no és igual a 55/45. El de la dreta sí, on 780/540 = 65/45.

Amb el gràfic de l’esquerra es pot interpretar que ambdues variables han evolucionat gairebé en paral·lel, que tenen pendent similar. La realitat és que el pendent dels “treballadors” és superior al d’”empreses”. L’increment en el període sencer ha estat del 28% i 13%, respectivament. La interpretació real és que el nombre d’empreses hauria crescut, i els treballadors ho han fet en més proporció (com mostra el gràfic de la dreta) amb el que ha augmentat la dimensió mitjana de les empreses. Els dos primers gràfics no mostren ben bé això.

Altres coses que poden millorar el gràfic, que guiïn al destinatari a l’hora de fer-ne una “lectura” i que li donin informació sense que hagi de pensar, són, per exemple: mostrar el valor de les variables per cada any i posar amb el mateix color tots els ítems de cada variable (nom, xifra, eix d’ordenades,..).

Distribució de respostes

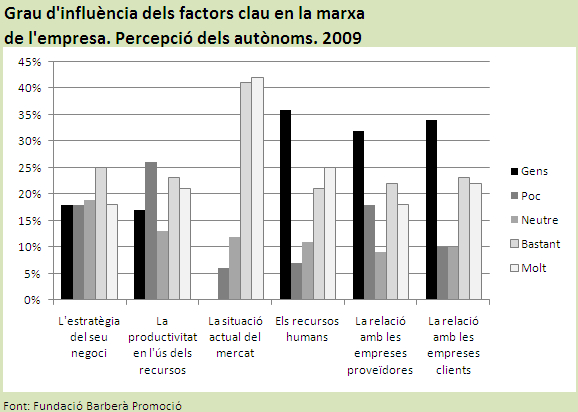
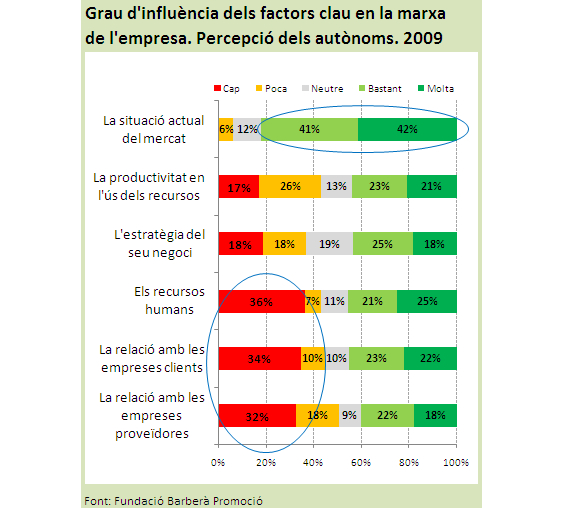
És possible graficar força dades com quan volem reflectir la distribució de respostes (molt, bastant, neutre, poc, cap) per a diversos ítems d’una mateixa pregunta. Fer-ho com el següent gràfic, relatiu al grau d’influència de diversos factors en la marxa d’una empresa, segons una enquesta a autònoms, implica un esforç de lectura.

Per ajudar al lector es poden fer les següents millores:

-      Barres en lloc de columnes, que en aquest cas ajuden a la lectura atès que estem acostumats a llegir d’esquerra a dreta.

-      Millor barres acumulades donat que es tracta d’una distribució percentual de respostes.

-      Atribució de les xifres a cadascuna de les respostes.

-      Atribució de colors estil “semàfor”.

-      Ordenar els ítems segons respostes de més a menys influència (per això ponderar el nombre de respostes atribuint un valor a cadascuna (cap=1, poc=2, ..., molt=5).

-      Si a més utilitzem cercles o fletxes podem fer que l’usuari es centri en la informació més rellevant o diferenciadora.

Així del gràfic se’n desprèn més fàcilment que el factor relativament més influent amb diferència entre els exposats és la situació del mercat. El segueixen dos factors que tenen similar grau de resposta entre cap-poca i bastant-molta influència, la productivitat i l’estratègia. Finalment els tres factors relativament menys influents serien els recursos humans i la relació tant amb les empreses clients com les empreses proveïdores.

Observatori econòmic i social. Fundació Barberà Promoció Ajuntament de Barberà del Vallès